Algebra, fractions, graphs!

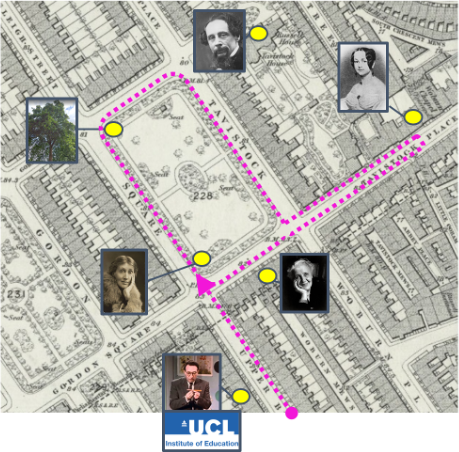
Phew. [1]An 1850s map of Tavistock Square illustrating the walking route from the Institute of Education, where Caleb Gattegno researched learning with Cuisenaire rods, to the statue of Virginia Woolf, the tree in the West corner, and the original sites of Charles Dickens’ house, the first English-speaking Kindergarten, and the Tavistock Clinic. Click the footnote to see an image in the footnotes tab.

I lasted two years as a mathematics teacher. Well, a year’s training and a year’s teaching. The most stressful job I’ve ever had. And in the rare, fleeting moments when it felt like it was going well, the best job I’ve ever had. I don’t know what the students made of it all. Maths lessons can be a nightmare for a lot of children. And a lot of teachers for that matter. So much anxiety. [2]Anxiety has been long-studied in psychology since Freud. Clinical definitions vary, but typically involve three dimensions: a subjective emotion of dread or foreboding, physiological symptoms of tension such as raised blood pressure and sweating, and a behavioural response of escape or avoidance (Ohman 1993, p.574). Anxiety may be contrasted with fear in that it concerns future rather than present events, it is in a sense unresolved fear, the cause of which one has not been able to escape. Click the footnote to see more information.

In Kindergarten, children seem quite happy playing with blocks, or running around outside in nature, playing games, and singing songs. Then something happens in primary school when formal maths lessons start.  I wonder if there’s some way of reconnecting with that spirit of kindergarten. [3]In England most children attend educational settings full-time from age 3 to 4, with compulsory full-time primary school education beginning in the Autumn term following the child’s 5th birthday, the start of Year 1 of primary school. The Early Years Foundation Stage (EYFS) curriculum covers birth to 5 years, when children move on to the primary curriculum, which includes a detailed programme of study specifically for mathematics which continues to the GCSE Mathematics examination usually taken at age 16. In the guidance for the EYFS curriculum, Development Matters, the word ‘play’ is mentioned over 150 times. In the guidance for the primary mathematics curriculum from Year 1 to Year 6, the word ‘play’ is mentioned only once, in relation to number games in Year 1. Click the footnote to read more.

That’s where I trained, on the left, the Institute of Education, here in Bloomsbury in London. A huge, modernist building, made of big concrete blocks, like some kind of Minecraft castle.

The building is like a grid, as if it was designed on squared paper, so many square windows, in a long row, hard to count.
They say the corridors are so long if you lie down and look along the floor, you can see the curvature of the earth! Hmm I wonder if that’s true. Fortunately, I know a man on the inside who can let me in. [4]“…the Institute’s Secretary Willis Dixon wrote: “We did not want long corridors, in which if you lie on the floor you can detect the curvature of the earth.” Click the footnote to read more.

So I’m here on the 7th floor. At the end of the corridor. I’ll start here. 1 2 3.

So let me think. Metres. After the French revolution they wanted a universal unit of measurement, that wasn’t decreed by a king. So, they based it on the Earth. At first people suggested the equator. [But others said no, the equator was against the principle of equality, because the equator only went through some countries. Instead, they decided it must be the distance from the equator to either pole because that line could be drawn through every country. So, they decreed, in 1793, that a new unit, the centimetre, was a billionth of the distance from the equator to the north pole. Bearing in mind no one had been to the north pole yet. But they reckoned they could work it all out using geometry. [5]Click the footnote to see images of some of the physical reference objects used in the introduction of the metric system in France in the 1790s.

A hundred and thirty seven, that’s the last bit.

OK that’s a hundred and thirty-seven metres long. In computer friendly binary numbers that’s 10001001. I’ve propped open the doors so I can see all the way down the length.

Hang on a sec. Here I am shouting from the other end!

It’s really long. And if I lie down. I’m just pressing my eye against the floor. It’s hard to tell because the carpet is a bit fuzzy. But it looks. It looks completely dead flat right to the end. No curve at all I can see.

I’ve got some little one-centimetre maths cubes here to help me work it out. So a billion centimetres from the equator to the north pole – that’s a billion of these one-centimetre cubes laid end to end, would end up curving round the Earth ninety degrees. So, a billionth of ninety degrees curvature per centimetre. Which over a hundred and thirty-seven metre corridor comes out at about a millimetre. Perhaps the world is a lot flatter than I thought. [6]The curvature according to this calculator over 137 metres would be approximately 1 centimetre, the same as a 1cm white Cuisenaire cube. In the podcast I have used some poetic licence to estimate this as about a millimetre, following a calculation error involving the misplacement of a decimal point. Click the footnote to read more.

OK so I could have worked that out, without smelling the carpet at the IoE. But then I wouldn’t have. Well, I wouldn’t have smelt the carpet at the IoE.

A lot of the roots of mathematics are in nature. Geo-metry. Literally Earth-measuring. Geo – Earth. And metry, metre, measure, from the same root word as mens, month, moon. As in commensurate. The full moon, quarter moon, new moon. Earth, moon and sun. Two bodies orbiting in space, and the pull of the third. The three-body problem. Or is it a problem [7]The problem of predicting the trajectories of two bodies orbiting each other in space, such as the Earth and Sun, can be solved mathematically with Newtonian mechanics. However, the introduction of a third body generates chaotic movements, and this so-called Three-Body Problem has not been solved. Click the footnote to read more.

And since ancient times humans have arranged giant stone blocks to measure the movements of the stars.

Male Druid: By the power of star and stone. Welcome everyone to Stanton Drew, to celebrate this winter solstice.[8]Many prehistoric stone circles in Britain and Ireland appear to be aligned with sunrise on the longest day of the summer solstice, and/or sunset on the shortest day of the winter solstice, which is always exactly the opposite direction. So it is sometimes difficult for archaeologists to tell which solstice was of most significance to the builders. Click the footnote to read more.

[INTERLUDE] Once upon a time there was a [beat] And it split into two [beat].

So I’m crossing the road now into Tavistock Square. I say square, geometrically speaking it is more of a rectangle, twice as long as it is wide. And when they first developed it in the early 1800s, technically they weren’t selling the square so much as the Georgian townhouses around it, which are about four stories high. So, if anything its more of a cube or a cuboid. Or perhaps a parallelopiped. But Tavistock Cuboid probably didn’t sound such an attractive address in those days, so Square it is.

There are lots of these squares round here, kind of tiling this part of London, Gordon Square, Russell square, Bedford Square. Usually named after the original landowners, or their wives.

Here there are still the original townhouses, with their classical Georgian architecture, based on musical harmonies. [9]Architects such as John Wood the Elder who designed many of the Georgian streets in Bath, as well as drawing on classical Palladian architecture were also influenced by the geometry of stone circles such as Stanton Drew and Stonehenge. Click the footnote to read more.

Goethe called architecture ‘frozen music, and music ‘liquid architecture’. [10]Goethe saw music as entwined with Nature, Science and philosophy. Click the footnote to read more.

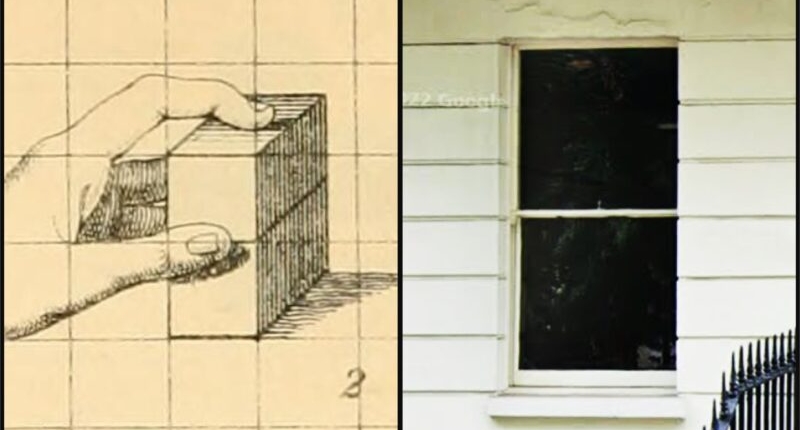
So, for instance if you look at the windows, they’re all the same width. On the top floor they’re square. [SFX: musical octave]. Lower down their double height – in music double the pitch is the same note an octave higher. And below that they are triple height. This ratio, of 2 to 3, is one of the most common harmonies in music. [11]The Pythagoreans of Plato’s time believed that plucking a string length divided by powers of 2 (2, 4, 8…) and powers of 3 (3, 9, 27…) resulted in harmonious musical intervals, which resonated with the cosmos, and they used the ratios of these numbers to generate the musical scale. Click the footnote to read more.

The ancient Greeks believed that 2 was the female principle and 3 the male. And that the harmonies of these vibrations resonated with their gods, the planets, in the heavens. [12]Newton was educated in Plato’s musical cosmology and when he studied the rainbow colours generated by sunlight passing through a triangular prism, he believed the frequencies of the spectrum should resonate with the seven tones of the musical scale, so he divided the rainbow into seven colours, corresponding to the notes A B C D E F G, illustrated in his c1665 sketch found in the Footnote Extras tab. Click the footnote to read more. [13]Gianluca Foschi has recreated the tones and ratios implied by the creation story in Plato’s Timaeus as a musical animation, as part of his PhD, based partly on the study of the monochord in Ancient Greece by Creese (2010).

And if you run a stick around the double length window, tapping each corner, you would get a double length beat, followed by a single beat along the short side. A threeness in the twoness. Like the rhythm of a waltz, or a heartbeat. Like the rhythm of the corners walking round Tavistock Square. Or dancing round it! [14]The harmonic series, the series of frequencies that a taut string, or column of air in a wind instrument, naturally resonates in when vibrated. Click the footnote to read more. [15]The pitches of the first three notes of Sunrise from Richard Strauss’s tone poem Also sprach Zarathustra, used in the opening scene of Stanley Kubrick’s 1968 film, 2001: A Space Odyssey, are an example of the start of the harmonic series in the ratio 2:3:4. Click the footnote to read more.

But the so-called irrational harmonies that didn’t fit these female-male two-three ratios, like the side of the square, with its diagonal caused the Ancient Greek philosophers problems.[16]The Platonic ‘lambda’ of two and three, squared and cubed, can be seen inscribed in the dress of the figure of ‘Arithmetica’ in one of the earliest printed mathematics textbooks, Margarita Philosophica, published in 1508. Click the footnote for an image. [17]YouTuber Mathologer offers a novel visual proof that length of the diagonal of a square – the square root of 2 – and the diagonal through the centre of a cube – the square root of 3 – are irrational numbers, that is, they cannot be expressed as a the ratio of any two whole numbers, so cannot be written exactly in our standard decimal number system. Click the footnote to read more.

And all around, trees, soar up through the top of the cuboid.

I’ve been looking at mathematical blocks so long I’m starting to see cubes crystallising everywhere!

[INTERLUDE] Once upon a time there was a [tone] And it split into two. And it split into two. And it split into two. Once upon a time there was a [tone] And it split into three. And it split into three. And it split into three.

Here I am in the south corner of the square, next to a bronze statue of Virginia Woolf’s head. With blank pupilless eyes, looking haunted and melancholy, gazing north, diagonally across the square. [18]There is a quote on the statue of Virginia Woolf in Tavistock Square from her diaries: “Then one day walking round Tavistock Square I made up, as I sometimes make up my books, To the Lighthouse; in a great, apparently involuntary, rush.”

Virginia Woolf used to live here with her husband Leonard Woolf in the 1920s and 30s, at number 52.
While they were living here Virginia fell in love with Vita Sackville West, and wrote a novel about her and for her, Orlando, the romantic adventures of a time-travelling, 300-year-old, gender-changing English aristocrat.

The Woolfs’ circle of artistic friends, the Bloomsbury set, had lots of love affairs and relationships between themselves. There is a book about them called ‘Living in Squares, loving in triangles.’ Full of the hopes, anxieties and sometimes chaotic balancing of love triangles. The relationship with another couple’s relationship.

And Virginia would compose her novels walking along this path around Tavistock Square. I’m going to follow in her footsteps, guided by her words.

Virginia Woolf: Words, English words, are full of echoes, memories, associations. They’ve been out and about on people’s lips, in their houses, in the streets, in the fields for so many centuries… Words live in the mind, and how do they live in the mind, variously and strangely much as human beings live, ranging hither and thither, falling in love and meeting together. [Link to source]

There’s a scent of flowers, roses. And the birds are in full song. Oh there’s a dead rat lying halfway across the path, I’ll take that as a good omen!

And there are so many trees. Here on the next corner, the west corner, is one of the tallest, it must be over a hundred, maybe two hundred years old.

It would have been here when Virginia Woolf was walking around this path. Maybe she even paused to put her hand on the tree trunk like this.

Virginia Woolf: My roots go down to the depths of the world, through earth dry brick, and damp earth, through veins of silver and lead. My hair is made of leaves. I am rooted to the middle of the earth. The roots make a skeleton on the ground, with dead leaves heaped in the angles. [Link to source]

[INTERLUDE] Once upon a time there was a seed, that split into two, that split into two. Once upon a time there was a branch, that split into two branches, that split into two.

Walking over to the north corner, there’s a plaque, ‘Charles Dickens, novelist, lived in Tavistock House near this site, 1851-1860’. That must have been a grand house, he was at the peak of his success, and lived there with his wife Catherine and their ten children.

Then in 1858 Catherine opened a mysterious packet, which a jeweller had accidentally delivered to Dickens’ home address. And inside she found a gold bracelet with a note from Charles to his 18-year old lover, Ellen Ternan, an actor in one of his plays. The Dickens’ marriage broke down, and Charles eventually forced Catherine to move out, and leave their children with him.

While he was living here Dickens started his own weekly magazine, Household Words, to serialise his new novel, Hard Times, with its satire of Victorian education.

Gradgrind character: Now, what I want is Facts. Teach these boys and girls nothing but Facts. Facts alone are wanted in life. Plant nothing else, and root out everything else. You can only form the minds of reasoning animals upon Facts; nothing else will ever be of any service to them. [Link to source]

The magazine also published articles on Victorian London life. There was a new kind of school for young children, opened just around the block, by the east corner of the square, almost backing onto Dickens garden, he could probably hear the children playing.

The school was based on playing with simple wooden blocks, singing and dancing, and spending time in nature.
Dickens loved it, championing the new play-based approach in his magazine:

Household Words article: With these forms of the cube, sphere, and cylinder, there is a great deal to be done, and learnt. They can be played with at first according to the child’s own humour: will run, jump, represent carts or anything. A child will see fishes in stones, and be content to put a cylinder upon a cube, and say that is papa on horseback. [Link to source]

He would have walked along this side of the square to visit the school.

Here it is, it’s now a café. In 1853 this is the spot where the first English-speaking Kindergarten was opened by two refugees from Germany, Bertha and Johannes Ronge.

Bertha had divorced her husband in Germany to flee to London with her lover Johannes, who was a defrocked Catholic priest, and anti-establishment activist, wanted by the German authorities. [19]The UCL Bloomsbury project has information about the Ronge’s Kindergarten, also known as a ‘Humanistic’ school, including a reference to the following quote from an article in the Lloyd’s Weekly Newspaper of 31st July 1853: “The Humanistic community, established by Mr. Ronge, the German religious reformer, took the premises of the house, 23 (sic)Tavistock Place, Tavistock Square, to hold there weekly meetings of cultus and general instructions. On the 14th inst., a gentleman was engaged in painting the solar system on the ceiling of the meeting-hall, adjoining the garden: two large stones were thrown at him from behind the walls enclosing the garden, and broke two squares of glass in the window; a few minutes later, another big stone was hit at Mr. Ronge's head, sitting then and writing in the adjoining small room, without, however, succeeding in doing any bodily damage to any one. A policeman was called in, examined the premises, and took away with him the stones, since there was no other mischief done.” Click the footnote to read more.

Bertha had studied the revolutionary educational ideas of Friedrich Froebel, the inventor of kindergarten, back in Germany. There Kindergarten had recently been outlawed. So, the Ronges decided to open a Kindergarten here in London.

Karl Marx, another German exile, lived a few blocks away, and couldn’t stand Johannes:

Karl Marx: Johannes Ronge.. is certainly not the author of the Book of Revelations. There is nothing mysterious about him, he is banal, hackneyed, as insipid as water, luke-warm dishwater. [Link to source]

But then, by spreading Froebel’s ideas, arguably the Ronges’ Kindergarten revolutionised education more than Marx ever did.

When Bertha’s sister Margarethe came to visit, Johannes introduced his friend Carl Schurz to her, and the two fell in love and got married, and emigrated to America, where they opened the first Kindergartens there. And the movement spread around the world. [20]Carl Schurz, who like his friend Johannes Ronge was a political exile from Germany in London, was introduced by Johannes to Bertha’s sister Margarethe. He recounts their betrothal in his memoir: “When Margarethe and I met in the Brüning salon, it seemed to go without saying that we belonged to each other. We gravitated to each other. This was also noticed quietly by the rest of the gathering. When I stepped up to Margarethe and began to speak with her, the others regularly drew back from us immediately and left us alone, which we found not in the least embarrassing. I noticed a couple of times that then the eye of the good Baroness touched us with an expression of special satisfaction. When I needed to take Margarethe to the door of her residence one evening, and we walked by the door and strolled entirely alone on a solitary evening walk, we really did not have much new to say to each other. What we felt for each other we already knew even without having said it. We found in ourselves the urge to share with each other much from our pasts. And so we wandered for a good few hours through the still streets, even though a light rain trickled down, and we did not have an umbrella with us. We later often told our children how their mother that night wore a hat with a green veil whose color ran, and when we finally came back to her door and I said good night, I found the soaked veil had drawn speckles and stripes of green on her face. We parted with the mutual assurance that we were now engaged.” Click the footnote to read more.

Froebel had a lonely childhood, his mother died when he was a baby, and his father was a stern Lutheran pastor. Growing up in a village in the Thuringia forest in Germany, he would spend hours playing alone in the garden or wandering in the woods, as if finding comfort in connecting with Mother Nature. [21]“When I was a Boy, and my sense for what is in nature was all awakening within me, I discovered a little flower, under a hedge of white roses in my Father’s garden; it was very difficult to see it at all; it had five petals and was red, with five golden points in the middle of it. It was a simple child of nature, and a hundred far more beautiful flowers were to be found all over the garden, tended by my Father’s careful hand, while that one had been allowed to bloom unnoticed, in a corner out of sight. Yet it was just this flower which riveted my attention more than all the rest; for when I looked down into its coronet, and between the little golden stars, I could fancy I was looking down into endless depths. I have looked into it for hours at a time, during months and years when the flower was in bloom: it seemed to me always to be wishing to say something, and yet I could not understand it; yet I never got in the least tired of looking into it; I thought I should be sure to see something in it presently” (Froebel, 1879, p.125). Click the footnote to read more.

Then as a young man, he took a job as an assistant to a professor of crystallography in Berlin. And looking into crystals, and seeing their cubic structure, he had a transformative revelation. It was as if the crystals were speaking to him.

Friedrich Froebel: Many things, both old and new, My dear cube brings into view; So my cube much pleases me, Because through it so much I see. It is a little world. [Link to source]

He now saw that children playing with blocks create worlds in the same way that the Earth forms structures from crystals. Children in block play are imitating Nature.

And he saw in the form of the cube a pedagogical significance. The two-fold mirror symmetries of the cube – its top and bottom sides, back and front, left and right – resemble feelings, mirroring. Whereas the three-fold symmetry of the three edges meeting at each corner resembles new knowledge, a third perspective emerging from a two-fold relationship. [22]Froebel carefully designed a series of playthings he called ‘Gifts’, to be introduced to children sequentially from birth to around age 7. The first Gift, for babies, was a red yarn ball on a string, designed to resemble the mother’s breast. In the second Gift there was a similar sized ball of solid wood, along with a wooden cylinder and cube. By hanging the cylinder on its side from a string and spinning it, a sphere was revealed, and similarly by spinning the cube a cylinder appeared. Thus, the sphere could be said to be in the cylinder and the cylinder in the cube. So, the sphere – initially connected with the mother’s breast - could be demonstrated to children as transforming into the cube and vica versa. Similarly ‘Mother Nature’ can be seen to produce and consist of cubic crystal forms. In Gift 3 the cube is halved in each dimension to make 8 smaller cubes. In Gift 5 this becomes a 3 x 3 x 3 cube. Click the footnote for an image.

Froebel called his new school for young children a kindergarten, literally a ‘child garden’, because he believed children grow naturally, like trees, just as saplings need sun and water and fertile soil, they just need the right environment.

And simple wooden building blocks, so children could imitate Nature’s process of crystallisation in play, creating worlds with their imagination, now became central to Froebel’s Kindergarten pedagogy. His insight, that simple raw building blocks unleash children’s creativity more than finished toys, would inspire Lego over a century later. [23]“Here we meet a very great imperfection and inadequateness, the already too complex and ornate, too-finished plaything. The child can begin no new thing with it, cannot produce enough variety by means of it, his power of creative imagination, his power of giving form to his own idea, are thus actually deadened” (Froebel, 1895, p.122). Click the footnote to read more.

Children were encouraged to play with these blocks and make whatever they liked. Weather models of things in the world around them, or pleasing symmetrical patterns, or symbols like the letters in their name. Freely expressing their feelings and ideas. [24]In Froebel’s The Education of Man, he spends over twenty pages on the applications of crystallography to education. In particular, Froebel finds meaning in the two-fold and three-fold symmetries of crystals – noting that regular five-fold symmetries are all but absent in crystal forms. He thus finds deep significance in the five-fold symmetries of flowers and other forms of life, which he sees as a manifestation of a higher ‘life-energy’: “The life-forms, however, are by no means satisfied with ever more characteristic representation of the original directions, and the resulting numerical relations that yield crystal forms. By the removal of external tension the inner energy has been raised into life-energy, and higher activities must become manifest in the formations. Therefore, among vegetable as well as among animal life-forms, we observe soon the prevalence of numerical relations based on the number five, which play in crystals a very subordinate part, and appear only accidentally, as it were, and transiently.” (Froebel, 1886, p.190) Click the footnote to read more.” (Deleuze & Guattari, 1988, p.60)

The Ronges wrote a guidebook for kindergarten teachers, with illustrated examples, like a garden bench made out of eight cubes, which in play the children could story and world into an idyllic family scene

Kindergarten teacher: Let us make a seat in the garden. O  how warm is the air ! How bright is the sun! How lofty are the trees! Now papa and mamma can sit, while we gather pretty flowers in a nosegay. [Link to source]

The same eight cubes could also be used to conjure darker even horrific worlds, just as familiar to many children in Victorian London. So, the garden seat, by moving two cubes, may be transformed into a gravestone.

Kindergarten teacher: Here is a monument: did you ever see one? Where? In the cemetery, churchyard. Little Sarah may build one for dear little Fanny, who was burned to death ; she played with the fire, lighted bits of paper to look at the pretty sparks, and her clothes caught fire, and she ran about crying for help, but the fire would not wait, it burned more and more; she ran, the more it flamed; and when she was found, her dear face was disfigured, her hands and arms and neck were all burned to a cinder, and she soon died. [Link to source]

And this embodiment of both dreams and nightmares in blocks continues in online block play platforms such as Minecraft, with its creative mode:

Child: Minecraft and Lego is really similar, and you can make all sorts of different houses, flowers, you can spawn in trees. 

As well as its survival mode, where you may be attacked by zombies, and giant spiders ridden by skeletons. [25]Pettersen, Arnseth & Silseth have researched the post-digital worlds of Kindergarten children in the 2020s, where the boundaries between online and physical worlds are blurred. Click the footnote to read more.

As children, the artists George Braques and Piets Mondrian, the architects Frank Lloyd Wright and Le Corbusier, growing up at the end of the nineteenth century, were among the first generation to attend Kindergarten, creating worlds with Froebel’s cubes, and they would go on to invent cubism and modernist architecture, like the IoE. [26]“The Victorian childhood of the seminal Modernists coincided with the development and widespread embrace of a radical educational system that was a catalyst in exploding the cultural past, and restructuring the resulting intellectual panoply with a new world-view. It was never fodder for artistic argument over absinthe and Gauloises in Montmartre cafés, nor was it taught at the tradition-bound academies. It has been largely ignored because its participants — three to seven year-olds — were in the primary band of the scholastic spectrum. It was the seed-pearl of the modern era and it was called Kindergarten.” Click the footnote to read more.

And later at the IoE, in the 1960s, the Egyptian educator Caleb Gattegno developed a way of teaching language without speaking, ‘The Silent Way’, again using wooden blocks.

One day in 1953, Gattegno visited a primary school in Belgium, and saw the children learning maths using wooden rods, 1cm to 10 cm long, painted in different colours, invented by the teacher, George Cuisenaire. Cuisenaire was a musician, who noticed that children easily remembered melodies, so he coloured the blocks according to the harmonies they would make if they were strings on a violin. Sounds became colours.

Halving the string length makes the same note an octave higher, so he made a rod that was half or double the length of another the same shade. So, the 2 cm, 4 cm and 8 cm long rods were red, pink and brown, all reddish shades.And the 3 and 6 were greenish shades, and 5 and 10 yellowish.

Sounds became colours.Colours now became lengths.

And, like Froebel, Gattegno had a kind of epiphany. He realised these blocks could be used for teaching all sorts of things. The meaning of the blocks could be transformed, they could become anything.

Gattegno: Now, start with the little white one and go up. Say the colours. White, red, light green, crimson, yellow.

The meaning of the blocks could be transformed. They could become anything.

Gattegno: Good. Now, let’s find their new names if we call the white one, ‘one’. If the white one is ‘one’, what’s the name of the red?

Children: Two!

Gattegno: And the light green? 

Children: Three!

Gattegno: And the purple? 

Children: Four!

Gattegno: And the yellow? 

Children: Five! [Link to source]

So, the white block could be the number one, and the red block the number two. Or the red block could be one, and the white block a half. Or the red block could be the colour red, or the sound ‘rrr’, or a stick, or a house, or a person, or fire, or ‘anger’. The green block could be the number three, or the colour green, or another person, or a tree, or ‘envy’. So, by naming the blocks at the start, almost like a kind of alchemy, the teacher could create a small world, full of relationships.

The red block is next to the green block. Or the girl is next to the tree, or the tree is taller than the girl, or the girl is angry with the boy, and so on.

Sentences and stories could be spoken by the students about the blocks, and their relationships, while the teacher was silent. Simply pointing to or re-arranging the blocks. Making worlds, and new relationships. The silent way.  The silent way has been adopted around the world as a way of teaching languages In Aotearoa-New Zealand, the silent way has been used for over forty years to teach Te Reo Māori, the Māori language.

Usually the first word attached to the wooden rods is the Māori word for stick, or tree, rakau. Over time they can become colours, things, feelings, people, family, family trees. [27]This clip of a Te reo Māori class using an approach based on Cuisenaire rods and the Silent Way (Gattegno, 2010) was recorded by Sifo Lakaw, who is researching ways of revitalizing indigenous languages, in particular the Pangcah language in Taiwan. Click the footnote to read more.

[INTERLUDE] Once upon a time there was a word, And it split into t-wo, And it split into th-r-ee.

On the same east corner of Tavistock Square as the Ronges’ Kindergarten, one of the first clinics to treat children’s anxiety was set up, the Tavistock Clinic, in 1920, based on the then still new theories of Sigmund Freud. The first English translations of Freud would be published by the Woolfs, who lived next door.

In Vienna Freud had studied his grandson Ernst as a toddler, and the way he would repeatedly throw objects away saying ‘here’ ‘gone’, ‘here’ ‘gone’ over and over. Freud thought Ernst was trying to relieve the anxiety he felt when his mother left the room, by projecting his feelings about his mother onto the object, and re-enacting the separation and re-union, in a way he could physically control.

For Froebel, too, in play a cube may be a caregiver:

Friedrich Froebel: What the little one has up to this time directly felt so often by the touch of  the mother’s breast – union and separation – it now perceives outwardly in an object which can be grasped and clasped. [Link to source]

At the Tavistock clinic Child psychologist Melanie Klein developed Freud’s idea of projection of phantasies, onto objects in play, and used it to explain the psychological benefits of play:

Melanie Klein: The brick, the little figure, the car, not only represent things which interest the child in themselves, but in his play with them they always have a variety of symbolical meanings as well … Play analysis had shown that symbolism enabled the child to transfer not only interests, but also phantasies, anxieties and guilt to objects other than people. Thus a great deal of relief is experienced in play and this is one of the factors which make it so essential for the child. [Link to source]

The cubes become symbols, which can be used to re-create, and to an extent control, our emotional worlds. Crystallising them into forms we can reshape, recrystallise.

So in play with blocks we can re-enact the holding and letting go of loving relationships. The tension and the relief. The twoness of a mutual gaze. The urge to connect, to transform and grow. And to turn away. From the twoness, the split oneness, of our first relationship, to a new third ‘other’. Second person to third person, from ‘you’, to a ‘they’, who becomes ‘you’ again. New symmetries and harmonies. Recrystallising relationships. Projecting onto things, or sounds, our fears, and our heart’s desires, and whatever we need to comfort ourselves through the cold, dark nights. And through mathematics lessons, in two and three, and geometry, and imagining what the unknown might be.

Friedrich Froebel: The ABC of things must precede the ABC of words, and give to the words their true foundations [Link to source]

And so along the fourth side of the square, back to the south corner, back to Virginia

Virginia Woolf: It was odd, she thought, how if one was alone, one leant to inanimate things; trees, streams, flowers; felt they expressed one; felt they became one. [Link to source] [28]Virginia Woolf and her husband Leonard ran their new publishing house the Hogarth Press from their house on Tavistock Square, and were the first official publishers of Freud in English translation. At first Virginia seemed sceptical of Freud: “I shall be plunged in publishing affairs at once; we are publishing Dr Freud, and I glance at the proof and read how Mr A. B. threw a bottle of red ink on to the sheets of his marriage bed to excuse his impotence to the housemaid, but – threw it in the wrong place which unhinged his wife’s mind, - and to this day she pours claret on the dinner table. We could go on like that for hours; and yet these Germans think it proves something – besides their own gull-like imbecility.” (Woolf, 1980, p.134-135) However over the years Woolf seemed to embrace some of Freud’s ideas: “My mother obsessed me, in spite of the fact that she died when I was thirteen, until I was forty-four. Then one day walking round Tavistock Square I made up, as I sometimes make up my novels, To the Lighthouse, in a great, apparently involuntary, rush. One thing burst into another. Blowing bubbles out of a pipe gives the feeling of the rapid crowd of ideas and scenes which blew out of my mind, so that my lips seemed syllabling of their own accord as I walked. What blew the bubbles? Why then? I have no notion. But I wrote the book very quickly, and when it was written, I ceased to be obsessed by my mother. I no longer hear her voice; I do not see her. I suppose that I did for myself what psychoanalysts do for their patients. I expressed some long felt and very deeply felt emotion. And in expressing it I explained it and then laid it to rest.” (Woolf, 1985, p.92)

[1] An 1850s map of Tavistock Square illustrating the walking route from the Institute of Education, where Caleb Gattegno researched learning with Cuisenaire rods, to the statue of Virginia Woolf, the tree in the West corner, and the original sites of Charles Dickens’ house, the first English-speaking Kindergarten, and the Tavistock Clinic:

---

[2] Anxiety has been long-studied in psychology since Freud. Clinical definitions vary, but typically involve three dimensions: a subjective emotion of dread or foreboding, physiological symptoms of tension such as raised blood pressure and sweating, and a behavioural response of escape or avoidance (Ohman 1993, p.574). Anxiety may be contrasted with fear in that it concerns future rather than present events, it is in a sense unresolved fear, the cause of which one has not been able to escape.

Maths anxiety was first formally identified and studied as ‘number anxiety’ in 1957 in a study of US college students (Dreger & Aitken 1957), but recently there has been increasing research focusing on younger primary children (Dowker, Sarkar & Looi 2016). For example two US studies – one of 5-7 year olds (Ramirez et al. 2013) and one of first-grade children (Harari, Vukovic & Bailey 2013) – found that many experience anxiety towards mathematics and that there is a negative correlation with maths performance. A UK qualitative study of 4-7 year olds found that attitudes were polarised, with some children expressing negative feelings about all aspects of numeracy (Petronzi et al. 2017).  There is also neuroscientific evidence of correlation between maths anxiety in children and activation of regions of the right amygdala associated with processing of negative stimuli (Young, Wu, & Menon 2012; Maratos et al. 2009), and Hunt, Bhardwa & Sheffield (2017) found a physiological correlation between primary children’s maths anxiety and blood pressure, with pressure rising according to the difficulty of the mental arithmetic task they were set. In a recent large-scale study of maths anxiety with over 1800 8-13-year-old children, Carey et al. (2019) found made several recommendations to address maths anxiety, including differentiating between cognitive and emotional anxiety, boosting teachers and parents own confidence around maths (especially among female teachers to counter gender stereotypes), and focusing on intervening to remediate maths anxiety at an early age, before a vicious cycle starts of anxiety inhibiting performance, causing anxiety and so on (p.16).

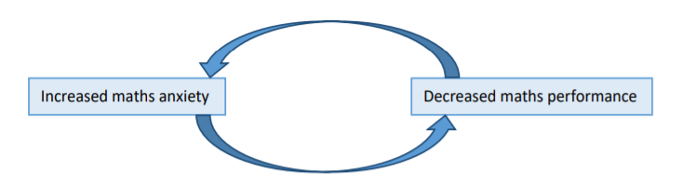
Figure 1. A vicious cycle of maths anxiety and inhibited performance (Carey et al. 2019, p.16)

Recent research by Connolly (2019) of over 9000 students in England found that female, Black and Asian students faced structural discrimination, judging from their misallocation into lower maths sets when starting secondary school compared with their results in standard tests at the end of primary. Female students were 1.5 times more likely than boys to be misallocated to lower sets, and Black and Asian students 2.4 and 1.7 times more likely respectively than White students, a pattern likely to exacerbate and compound anxiety felt from earlier experiences of inequalities and any institutional racism and sexism in primary schools.

---

[3] In England most children attend educational settings full-time from age 3 to 4, with compulsory full-time primary school education beginning in the Autumn term following the child’s 5th birthday, the start of Year 1 of primary school. The Early Years Foundation Stage (EYFS) curriculum covers birth to 5 years, when children move on to the primary curriculum, which includes a detailed programme of study specifically for mathematics which continues to the GCSE Mathematics examination usually taken at age 16. In the guidance for the EYFS curriculum, Development Matters, the word ‘play’ is mentioned over 150 times. In the guidance for the primary mathematics curriculum from Year 1 to Year 6, the word ‘play’ is mentioned only once, in relation to number games in Year 1.

---

[4] “…the Institute’s Secretary Willis Dixon wrote: “We did not want long corridors, in which if you lie on the floor you can detect the curvature of the earth”. (source)

---

[5] Images of some of the physical reference objects used in the introduction of the metric system in France in the 1790s can be seen in this article.

[6] This online tool calculates the earth’s curvature https://earthcurvature.com/ . The curvature according to this calculator over 137 metres would be approximately 1 centimetre, the same as a 1cm white Cuisenaire cube. In the podcast I have used some poetic licence to estimate this as about a millimetre, following a calculation error involving the misplacement of a decimal point.

---

[7] The problem of predicting the trajectories of two bodies orbiting each other in space, such as the Earth and Sun, can be solved mathematically with Newtonian mechanics. However, the introduction of a third body generates chaotic movements, and this so-called Three-Body Problem has not been solved.

---

[8] Many prehistoric stone circles in Britain and Ireland appear to be aligned with sunrise on the longest day of the summer solstice, and/or sunset on the shortest day of the winter solstice, which is always exactly the opposite direction. So it is sometimes difficult for archaeologists to tell which solstice was of most significance to the builders.

---

[9] Architects such as John Wood the Elder who designed many of the Georgian streets in Bath, as well as drawing on classical Palladian architecture were also influenced by the geometry of stone circles such as Stanton Drew and Stonehenge.

---

[10] Goethe saw music as entwined with Nature, Science and philosophy.

---

[11] The Pythagoreans of Plato’s time believed that plucking a string length divided by powers of 2 (2, 4, 8…) and powers of 3 (3, 9, 27…) resulted in harmonious musical intervals, which resonated with the cosmos, and they used the ratios of these numbers to generate the musical scale.

---

[12] Newton was educated in Plato’s musical cosmology and when he studied the rainbow colours generated by sunlight passing through a triangular prism, he believed the frequencies of the spectrum should resonate with the seven tones of the musical scale, so he divided the rainbow into seven colours, corresponding to the notes A B C D E F G, illustrated in his c1665 sketch below:

---

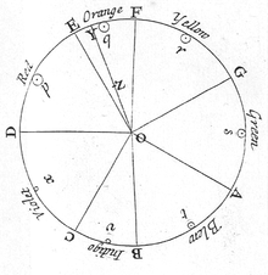
[13] Gianluca Foschi has recreated the tones and ratios implied by the creation story in Plato’s Timaeus as a musical animation, as part of his PhD, based partly on the study of the monochord in Ancient Greece by Creese (2010).

---

[14] The harmonic series, the series of frequencies that a taut string, or column of air in a wind instrument, naturally resonates in when vibrated, can be explored here.

---

[15] The pitches of the first three notes of Sunrise from Richard Strauss’s tone poem Also sprach Zarathustra, used in the opening scene of Stanley Kubrick’s 1968 film, 2001: A Space Odyssey, are an example of the start of the harmonic series in the ratio 2:3:4:

---

[16] The Platonic ‘lambda’ of two and three, squared and cubed, can be seen inscribed in the dress of the figure of ‘Arithmetica’ in one of the earliest printed mathematics textbooks, Margarita Philosophica, published in 1508:

---

[17] YouTuber Mathologer offers a novel visual proof that length of the diagonal of a square – the square root of 2 – and the diagonal through the centre of a cube – the square root of 3 – are irrational numbers, that is, they cannot be expressed as a the ratio of any two whole numbers, so cannot be written exactly in our standard decimal number system.

---

[18] There is a quote on the statue of Virginia Woolf in Tavistock Square from her diaries: “Then one day walking round Tavistock Square I made up, as I sometimes make up my books, To the Lighthouse; in a great, apparently involuntary, rush.”

---

[19]  The UCL Bloomsbury project has information about the Ronge’s Kindergarten, also known as a ‘Humanistic’ school , including a reference to the following quote from an article in the Lloyd’s Weekly Newspaper of 31st July 1853:

“The Humanistic community, established by Mr. Ronge, the German religious reformer, took the premises of the house, 23 [sic] Tavistock Place, Tavistock Square, to hold there weekly meetings of cultus and general instructions. On the 14th inst., a gentleman was engaged in painting the solar system on the ceiling of the meeting-hall, adjoining the garden: two large stones were thrown at him from behind the walls enclosing the garden, and broke two squares of glass in the window; a few minutes later, another big stone was hit at Mr. Ronge’s head, sitting then and writing in the adjoining small room, without, however, succeeding in doing any bodily damage to any one. A policeman was called in, examined the premises, and took away with him the stones, since there was no other mischief done.”

---

[20] Carl Schurz, who like his friend Johannes Ronge was a political exile from Germany in London, was introduced by Johannes to Bertha’s sister Margarethe. He recounts their betrothal in his memoir: “When Margarethe and I met in the Brüning salon, it seemed to go without saying that we belonged to each other. We gravitated to each other. This was also noticed quietly by the rest of the gathering. When I stepped up to Margarethe and began to speak with her, the others regularly drew back from us immediately and left us alone, which we found not in the least embarrassing. I noticed a couple of times that then the eye of the good Baroness touched us with an expression of special satisfaction. When I needed to take Margarethe to the door of her residence one evening, and we walked by the door and strolled entirely alone on a solitary evening walk, we really did not have much new to say to each other. What we felt for each other we already knew even without having said it. We found in ourselves the urge to share with each other much from our pasts. And so we wandered for a good few hours through the still streets, even though a light rain trickled down, and we did not have an umbrella with us. We later often told our children how their mother that night wore a hat with a green veil whose color ran, and when we finally came back to her door and I said good night, I found the soaked veil had drawn speckles and stripes of green on her face. We parted with the mutual assurance that we were now engaged.”  (source)

---

[21] “When I was a Boy, and my sense for what is in nature was all awakening within me, I discovered a little flower, under a hedge of white roses in my Father’s garden; it was very difficult to see it at all; it had five petals and was red, with five golden points in the middle of it. It was a simple child of nature, and a hundred far more beautiful flowers were to be found all over the garden, tended by my Father’s careful hand, while that one had been allowed to bloom unnoticed, in a corner out of sight. Yet it was just this flower which riveted my attention more than all the rest; for when I looked down into its coronet, and between the little golden stars, I could fancy I was looking down into endless depths. I have looked into it for hours at a time, during months and years when the flower was in bloom: it seemed to me always to be wishing to say something, and yet I could not understand it; yet I never got in the least tired of looking into it; I thought I should be sure to see something in it presently.” (Froebel, 1879, p.125)

---

[22] Froebel carefully designed a series of playthings he called ‘Gifts’, to be introduced to children sequentially from birth to around age 7. The first Gift, for babies, was a red yarn ball on a string, designed to resemble the mother’s breast. In the second Gift there was a similar sized ball of solid wood, along with a wooden cylinder and cube. By hanging the cylinder on its side from a string and spinning it, a sphere was revealed, and similarly by spinning the cube a cylinder appeared. Thus, the sphere could be said to be in the cylinder and the cylinder in the cube. So, the sphere – initially connected with the mother’s breast – could be demonstrated to children as transforming into the cube and vica versa. Similarly ‘Mother Nature’ can be seen to produce and consist of cubic crystal forms. In Gift 3 the cube is halved in each dimension to make 8 smaller cubes. In Gift 5 this becomes a 3 x 3 x 3 cube.

---

[23] “Here we meet a very great imperfection and inadequateness, the already too complex and ornate, too-finished plaything. The child can begin no new thing with it, cannot produce enough variety by means of it, his power of creative imagination, his power of giving form to his own idea, are thus actually deadened.” (Froebel, 1895, p.122)

---

[24] In Froebel’s The Education of Man, he spends over twenty pages on the applications of crystallography to education. In particular, Froebel finds meaning in the two-fold and three-fold symmetries of crystals – noting that regular five-fold symmetries are all but absent in crystal forms. He thus finds deep significance in the five-fold symmetries of flowers and other forms of life, which he sees as a manifestation of a higher ‘life-energy’:

“The life-forms, however, are by no means satisfied with ever more characteristic representation of the original directions, and the resulting numerical relations that yield crystal forms. By the removal of external tension the inner energy has been raised into life-energy, and higher activities must become manifest in the formations. Therefore, among vegetable as well as among animal life-forms, we observe soon the prevalence of numerical relations based on the number five, which play in crystals a very subordinate part, and appear only accidentally, as it were, and transiently.” (Froebel, 1886, p.190). Read more on the Resource tab.

Echoes of Froebel’s idea of heightened life-energy can be heard in Deleuze & Guattari’s concept of the index of territoriality and the deterritorialization of the organic stratum – for example DNA enables organisms to encode and decode more complex spatial structures and symmetries and reproduce them over time and space:
“A crystal displays this process in its pure state, since its form expands in all directions, but always as a function of the surface layer of the substance, which can be emptied of most of its interior without interfering with the growth. It is the crystal’s subjugation to three-dimensionality, in other words its index of territoriality, that makes the structure incapable of formally reproducing and expressing itself; only the accessible surface can reproduce itself, since it is the only deterritorializable part. On the contrary, the detachment of a pure line of expression on the organic stratum makes it possible for the organism to attain a much higher threshold of deterritorialization, gives it a mechanism of reproduction covering all the details of its complex spatial structure” (Deleuze & Guattari, 1988, p.60)

---

[25] Pettersen, Arnseth & Silseth have researched the post-digital worlds of Kindergarten children in the 2020s, where the boundaries between online and physical worlds are blurred.

---

[26]  “The Victorian childhood of the seminal Modernists coincided with the development and widespread embrace of a radical educational system that was a catalyst in exploding the cultural past, and restructuring the resulting intellectual panoply with a new world-view. It was never fodder for artistic argument over absinthe and Gauloises in Montmartre cafés, nor was it taught at the tradition-bound academies. It has been largely ignored because its participants — three to seven year-olds — were in the primary band of the scholastic spectrum. It was the seed-pearl of the modern era and it was called Kindergarten.”  (Source)

---

[27] This clip of a Te reo Māori class using an approach based on Cuisenaire rods and the Silent Way (Gattegno, 2010) was recorded by Sifo Lakaw, who is researching ways of revitalizing indigenous languages, in particular the Pangcah language in Taiwan.

---

[28] Virginia Woolf and her husband Leonard ran their new publishing house the Hogarth Press from their house on Tavistock Square, and were the first official publishers of Freud in English translation. At first Virginia seemed sceptical of Freud:

“I shall be plunged in publishing affairs at once; we are publishing Dr Freud, and I glance at the proof and read how Mr A. B. threw a bottle of red ink on to the sheets of his marriage bed to excuse his impotence to the housemaid, but – threw it in the wrong place which unhinged his wife’s mind, – and to this day she pours claret on the dinner table. We could go on like that for hours; and yet these Germans think it proves something – besides their own gull-like imbecility.” (Woolf, 1980, p.134-135)

However over the years Woolf seemed to embrace some of Freud’s ideas:

“My mother obsessed me, in spite of the fact that she died when I was thirteen, until I was forty-four. Then one day walking round Tavistock Square I made up, as I sometimes make up my novels, To the Lighthouse, in a great, apparently involuntary, rush. One thing burst into another. Blowing bubbles out of a pipe gives the feeling of the rapid crowd of ideas and scenes which blew out of my mind, so that my lips seemed syllabling of their own accord as I walked. What blew the bubbles? Why then? I have no notion. But I wrote the book very quickly, and when it was written, I ceased to be obsessed by my mother. I no longer hear her voice; I do not see her.

I suppose that I did for myself what psychoanalysts do for their patients. I expressed some long felt and very deeply felt emotion. And in expressing it I explained it and then laid it to rest.” (Woolf, 1985, p.92)

---

References

Carey, E., Devine, A., Hill, F., Dowker, A., McLellan, R., & Szucs, D. (2019). Understanding Mathematics Anxiety: Investigating the experiences of UK primary and secondary school students.

Connolly, P., Taylor, B., Francis, B., Archer, L., Hodgen, J., Mazenod, A., & Tereshchenko, A. (2019). The misallocation of students to academic sets in maths: A study of secondary schools in England. British Educational Research Journal, 45(4), 873-897.

Creese, D. (2010). The monochord in ancient Greek harmonic science. Cambridge University Press.

Deleuze, G., & Guattari, F. (1988). A thousand plateaus: Capitalism and schizophrenia. Bloomsbury Publishing.

Devine, A., Fawcett, K., Szucs, D., and Dowker, A. (2012). Gender differences in mathematics anxiety and the relation to mathematics performance while controlling for test anxiety. Behav. Brain Funct. 8, 1–9. doi: 10.1186/1744-9081-8-33

Dowker, A., Sarkar, A., & Looi, C. Y. (2016). Mathematics anxiety: What have we learned in 60 years?. Frontiers in psychology, 7, 508.

Dreger, R. M., & Aiken Jr, L. R. (1957). The identification of number anxiety in a college population. Journal of Educational psychology, 48(6), 344.

Froebel, F. (1879). Mother-play and Nursery Songs: With Notes to Mothers. Lee and Shepard.

Froebel, F. (1886). The education of man (Vol. 5). A. Lovell & Company.

Froebel, F. (1895). Friedrich Froebel’s pedagogics of the kindergarten: Or, his ideas concerning the play and playthings of the child (Vol. 30). D. Appleton.

Gattegno, C. (2010). Teaching foreign languages in schools: The silent way. Educational Solutions World.

Harari, R. R., Vukovic, R. K., & Bailey, S. P. (2013). Mathematics anxiety in young children: An exploratory study. The Journal of experimental education, 81(4), 538-555.

Hunt, T. E., Bhardwa, J., & Sheffield, D. (2017). Mental arithmetic performance, physiological reactivity and mathematics anxiety amongst UK primary school children. Learning and Individual Differences, 57, 129-132.

Maratos, F. A., Mogg, K., Bradley, B. P., Rippon, G., & Senior, C. (2009). Coarse threat images reveal theta oscillations in the amygdala: A magnetoencephalography study. Cognitive, Affective, & Behavioral Neuroscience, 9(2), 133-143.

Ohman, A. (1993). Fear and anxiety: Evolutionary, cognitive and clinical perspectives. Hand-book of Emotions, 511-536.

Petronzi, D., Staples, P., Sheffield, D., Hunt, T. & Fitton-Wilde, S. (2017). Numeracy Apprehension in Young Children: Insights from Children Aged 4-7 Years and Primary Care. Psychology and Education, 54(1).

Petronzi, D., Staples, P., Sheffield, D. et al. Further development of the Children’s Mathematics Anxiety Scale UK (CMAS-UK) for ages 4–7 years. Educ Stud Math 100, 231–249 (2019)

Pettersen, K., Arnseth, H. C., & Silseth, K. (2022). Playing Minecraft: Young children’s postdigital play. Journal of Early Childhood Literacy, 0(0).

Ramirez, G., Gunderson, E. A., Levine, S. C., & Beilock, S. L. (2013). Math anxiety, working memory, and math achievement in early elementary school. Journal of Cognition and Development, 14(2), 187-202

Woolf, V., Bell, A. O., & McNeillie, A. (1980). The diary of Virginia Woolf. Vol. 3, 1925-30. Penguin.

Woolf, V. (1985). Moments of being. Houghton Mifflin Harcourt.

Young, C. B., Wu, S. S., & Menon, V. (2012). The neurodevelopmental basis of math anxiety. Psychological science, 23(5), 492-501.

Listen to the full reprise composition

Listen to an Epilogue: A Space Odyssey

Stop-Motion Promotions for Episode (created by Gene!)

Video Resources

The Waves by Virginia Woolf

Audio Resources

Roland50 studio

Chrome music explorer

Audio clips of Caleb Gattegno

Publications

One, You, She: Object relations as grounding metaphors for learning mathematics

Musical bar-modelling – Designing Cuisenaire rod ‘object lessons’ to bring music back in harmony with mathematics

A Practical Guide to the English Infant Garden by Bertha and Johannes Ronge

Folding Froebel with Deleuze: Rethinking the significance of imitation in early childhood

Inventing Kindergarten

The UCL Bloomsbury Project on the Ronges’ Kindergarten

Selected articles by Caleb Gattegno

Te Whakapapa o te Reo i Roto i te Whūnau

Building Blocks – A Cultural History of Codes Compositions and Dispositions

Haüy, Weiß, Fröbel: the influence of nineteenth-century crystallography on the mathematics of Friedrich Fröbel’s kindergarten

A Thousand Plateaus by Deleuze & Guattari

Mathematics and the Body by De Freitas & Sinclair

A Handbook of Attachment

The Silence of the Body by David Pimm

Websites

Georges Cuisenaire and Cuisenaire rods

The Tongue of the Dog